플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)

플로이드-워셜 알고리즘은 다익스트라 알고리즘과 비슷하게 최단경로(shortest-path)를 탐색하는 알고리즘이다.

다익스트라 알고리즘 vs 플로이드-워셜 알고리즘

• 다익스트라 알고리즘은 하나의 정점에서 다른 모든 정점까지의 최단경로를 구하는 알고리즘이지만, 플로이드-워셜 알고리즘은 모든 노드간 최단경로를 구하는 알고리즘이다.
• 다익스트라 알고리즘은 가중치가 음수인 간선이 존재하면 사용할 수 없지만, 플로이드-워셜 알고리즘은 음수 간선이 존재해도 사용할 수 있다. 단, 음의 사이클(negative cycle)이 있을경우에는 플로이드-워셜 알고리즘도 사용불가능하다. (음의 사이클이 존재하면 벨만-포드 알고리즘 사용)

플로이드-워셜 알고리즘의 과정

플로이드-워셜 알고리즘은 그래프를 인접행렬로 나타내는 데에서 시작한다. 다음과 같은 그래프를 생각해보자.

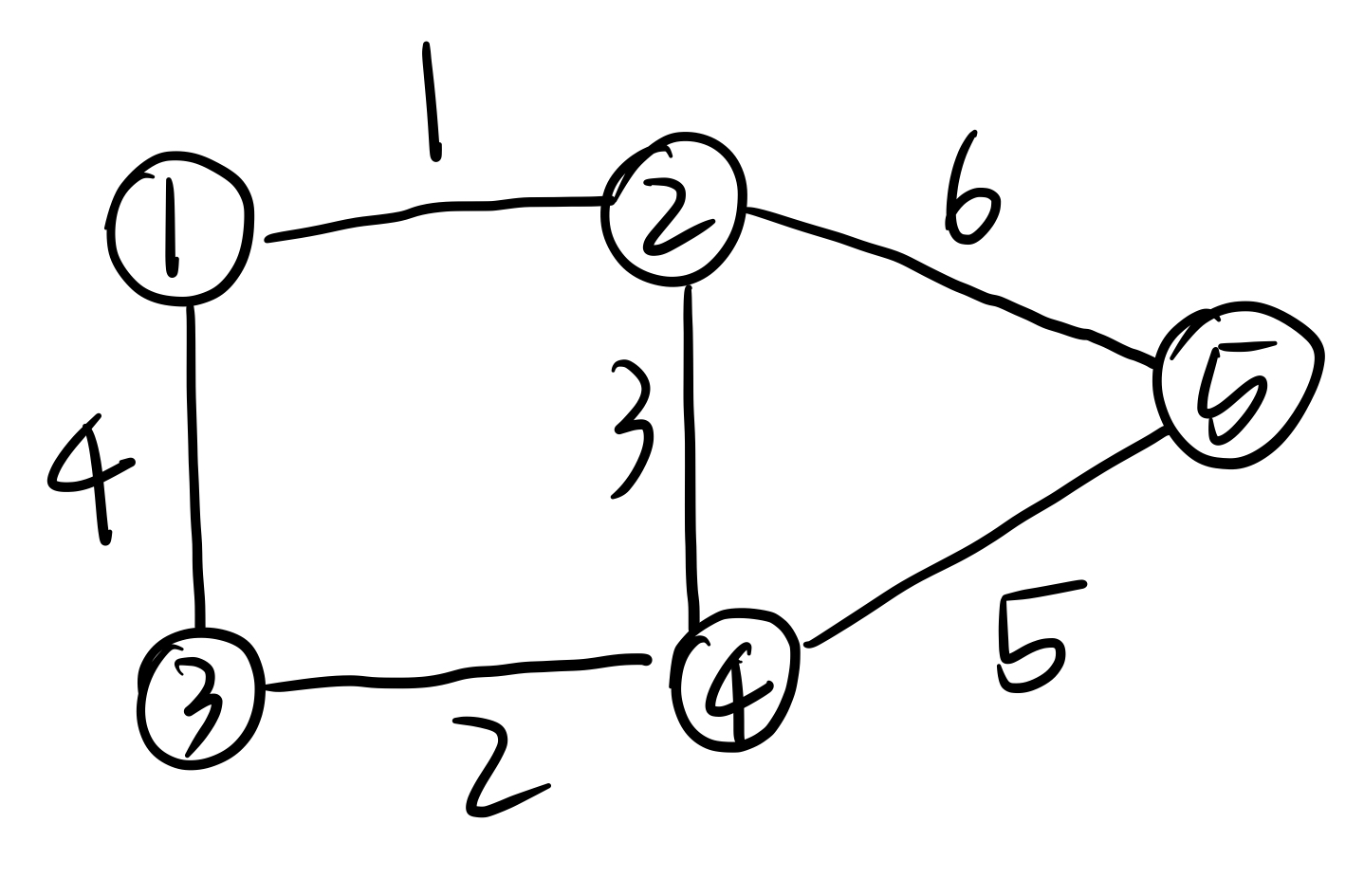
위 그래프를 인접행렬로 나타내면 다음과 같다.

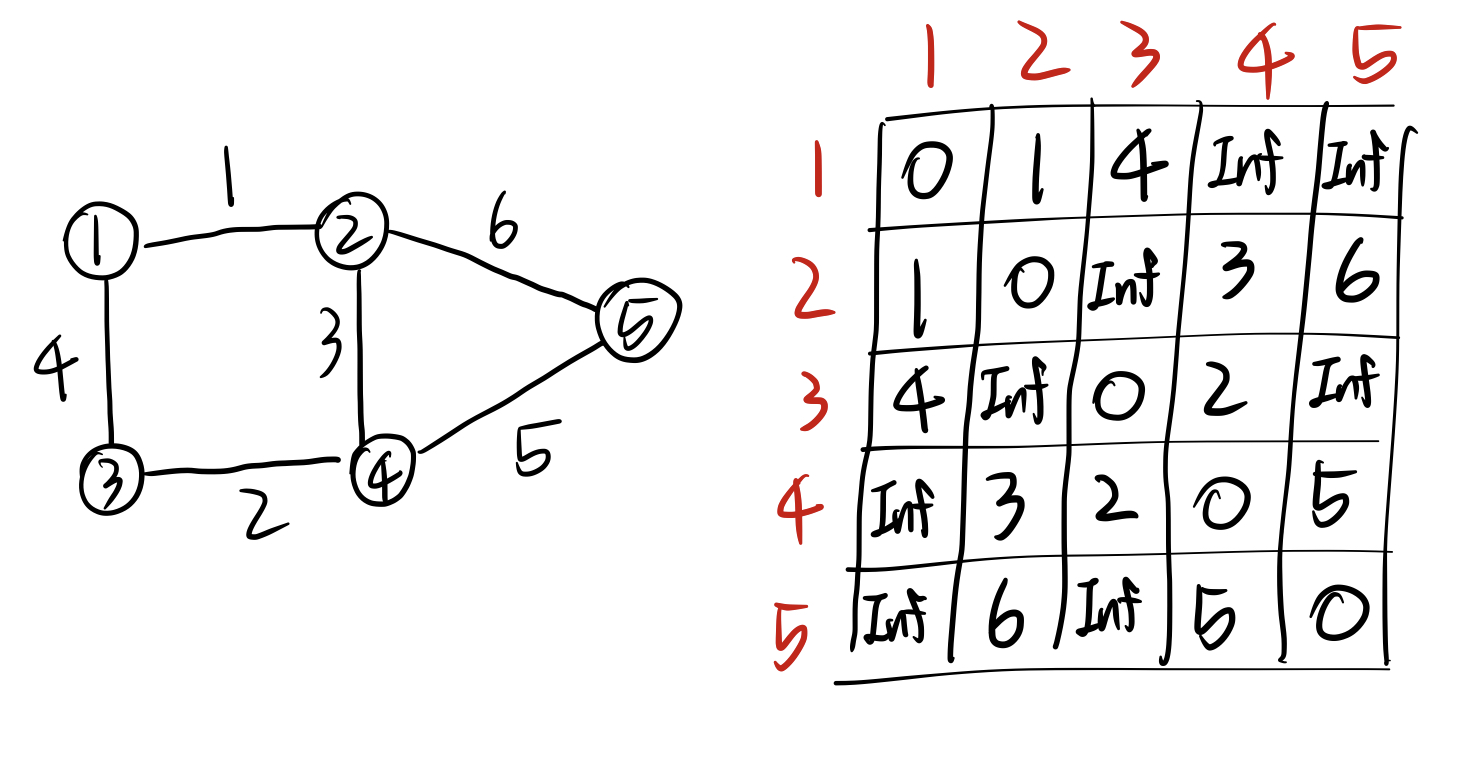
인접행렬에서 1행 3열은 1번노드에서 3번노드로 가는 비용(위 그래프에서는 4), 4행 2열은 4번노드에서 2번노드로 가는 비용(위 그래프에서는 3)을 담고 있다.

처음 인접행렬에 값을 채워넣을 때에는 단순히 해당 노드에서 곧장 갈 수 있는 노드만 생각한다. 다른 노드를 거쳐가는 간선은 생각하지 않는다는 뜻이다.

예를 들어 위 그래프에서 3번 노드에서 2번노드로 곧장 가는 길은 존재하지 않으므로 Inf(무한)으로 값을 채워넣는다.

인접행렬을 초기화 하고 나면, 모든 노드에 대해 해당 노드를 중간노드로 설정해 인접행렬의 값을 업데이트한다.

예를들어 위 그래프는 5개의 노드를 가지고 있으므로 1번노드부터 5번노드까지 모든 노드를 중간노드로 설정해보고 값을 업데이트 할 수 있으면 업데이트한다.

1번노드를 중간노드로 설정하는 경우를 살펴보자.

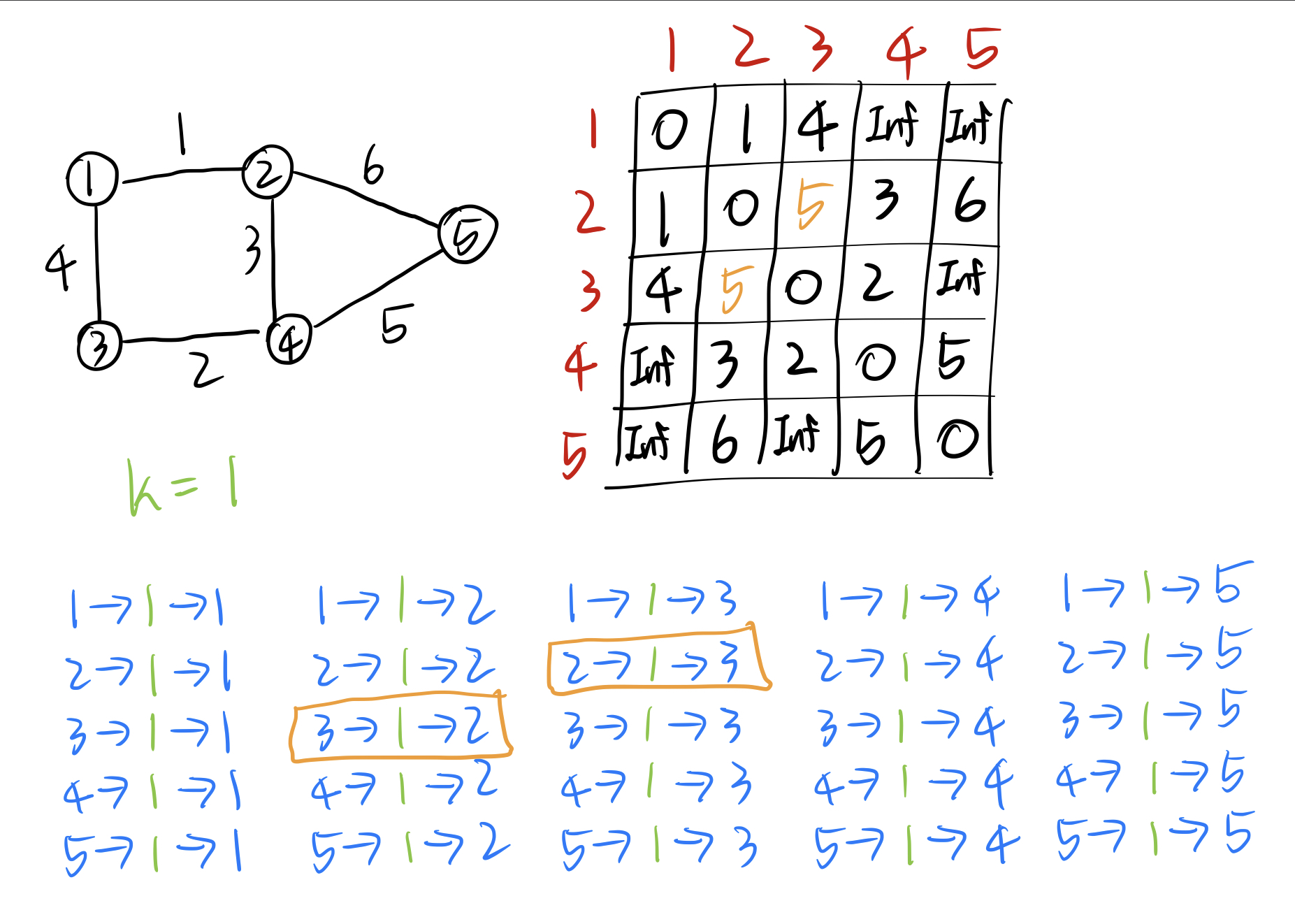
1번 노드를 중간노드로 하여 만약 그 값이 현재 인접행렬의 값보다 비용이 작다면 인접행렬의 값을 업데이트한다. 위 그래프의 경우에는 원래 3번노드에서 2번노드로 가는 길이 존재하지 않아 인접행렬의 값이 Inf였으나 1번노드를 거쳐가면 5(4+1)의 비용으로 Inf보다 작은 값이므로 인접행렬을 업데이트한다. (2번노드에서 3번노드도 동일)

다음으로는 2번노드를 중간노드로 설정하는 경우를 살펴본다.

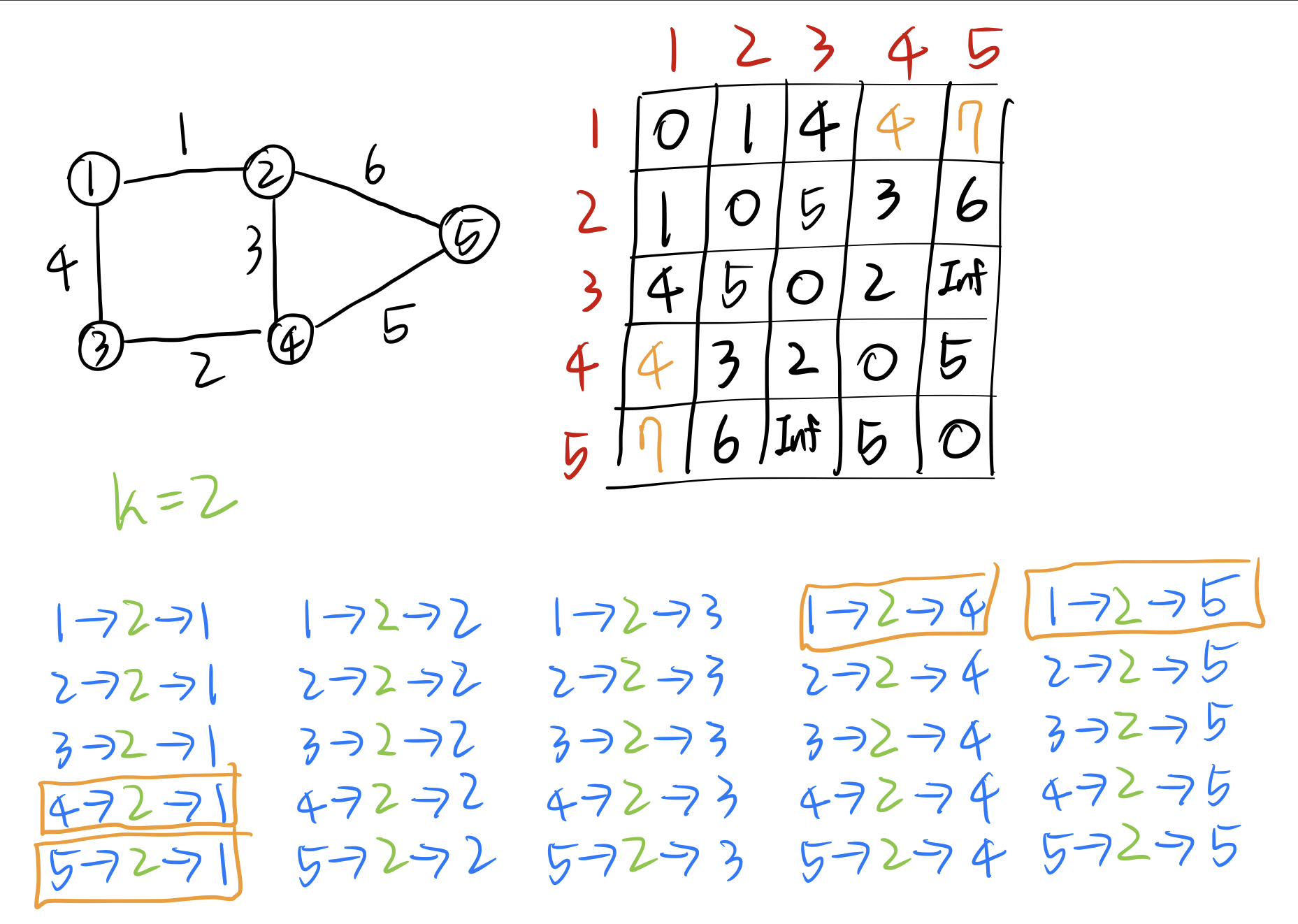
마찬가지로 2번노드를 중간노드로 했을때 현재 인접행렬 값보다 비용이 작다면 인접행렬의 값을 업데이트한다. 위 그래프의 경우에는 4번노드에서 1번노드로 가는 경우, 5번노드에서 1번노드로 가는 경우가 업데이트 되었다.(1→4, 1→5도 동일)

이 과정을 모든 노드에 대해 수행한다. 위 그래프의 경우 1번노드부터 5번노드까지 수행한다.

모든 과정을 마치고 나면 다음과 같은 인접행렬을 얻을 수 있다.

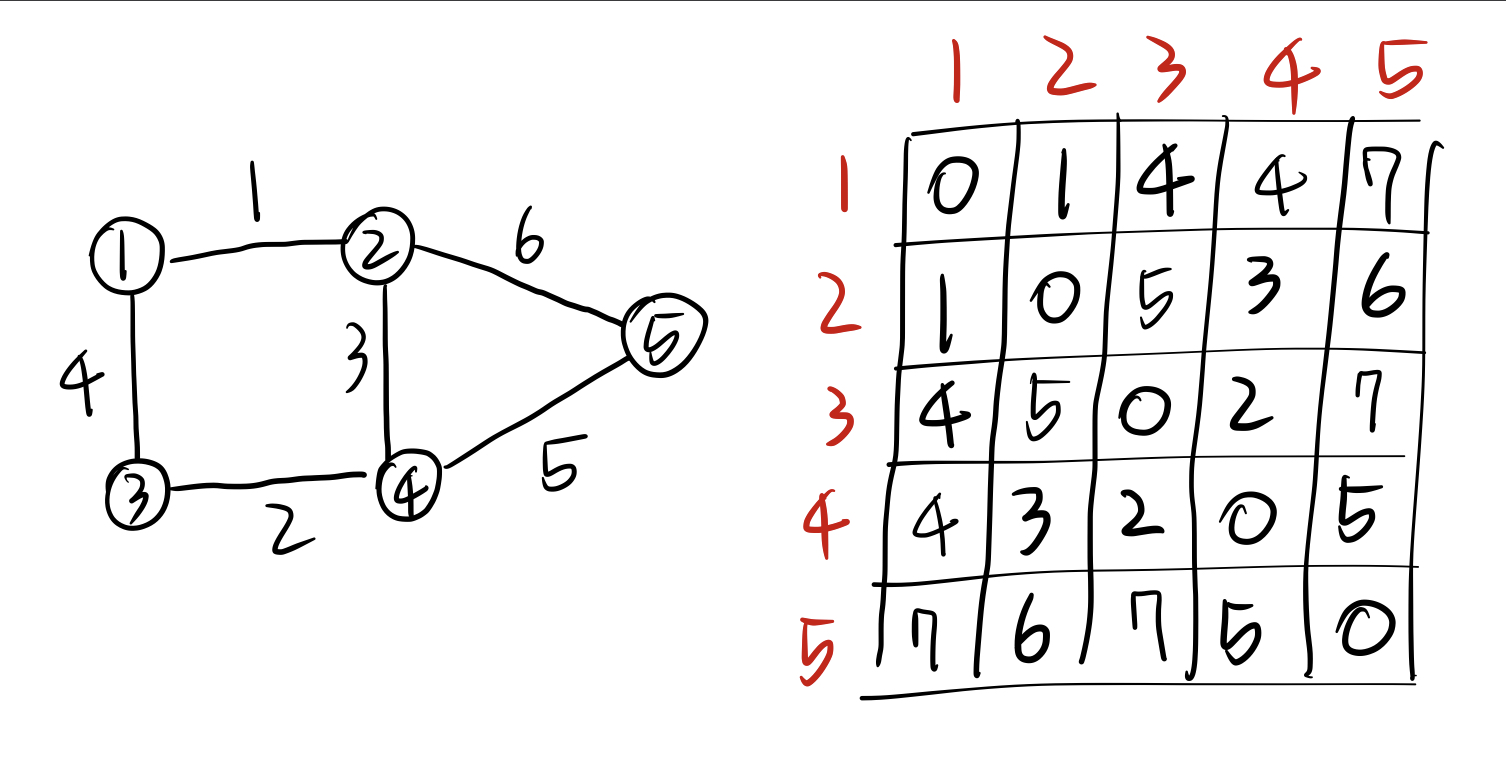
완성된 인접행렬의 값들이 모든 노드들간의 최단경로이다.

플로이드 워셜 구현

백준 11404번 - 플로이드

#include <iostream>

using namespace std;

int n, m;
int dist[111][111];

void floyd() {
  for (int k = 1; k <= n; k++)
    for (int i = 1; i <= n; i++)
      for (int j = 1; j <= n; j++)
        dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
}

int main() {
  cin.tie(0)->sync_with_stdio(0);

  cin >> n >> m;
  int a, b, c;

  for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++)
      if (i != j) dist[i][j] = 999'999'999;

  for (int i = 0; i < m; i++) {
    cin >> a >> b >> c;
    if (c < dist[a][b]) dist[a][b] = c;
  }

  floyd();

  for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++)
      dist[i][j] == 999'999'999 ? cout << 0 << " " : cout << dist[i][j] << " ";
    cout << "\n";
  }

  return 0;
}

플로이드 워셜 알고리즘의 구현은 Dynamic Programming을 통해 구현한다. 인접행렬의 점화식은 다음과 같다.

dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])

이때 dist[i][j]는 i번노드에서 j번 노드로 가는 경로의 비용이고, k는 중간노드이다.

위에서 설명할 때는 무방향 그래프를 예시로 들었지만, 문제 예시는 방향이 있는 그래프이다. 크게 다를건 없다.

인접행렬을 충분히 큰 값으로 초기화하고, 그래프를 입력받은 뒤 플로이드-워셜 알고리즘을 한 번 돌린 후 문제의 조건에 맞게 출력하면 문제를 해결할 수 있다.

시간복잡도

플로이드-워셜 알고리즘의 시간복잡도는 구현코드의 삼중반복문을 보면 알 수 있겠지만 O(N^3)이다. N번의 탐색동안 N^2번 값을 비교하여 배열을 업데이트하기 때문이다.

사용 팁

• 플로이드-워셜 알고리즘은 음수 간선의 존재를 감지할 수 있다. 간단하게 자기 자신에게 가는 간선의 비용을 검사하면 된다. 모든 간선이 양수라면 자기 자신에게 가는 간선의 비용은 0임이 자명하다. 하지만 만약 음수 간선이 존재한다면 0이 아닌 음수의 값이 나타나게 되므로 이를 이용해 주어진 그래프에 음수 간선이 존재하는지 확인할 수 있다.

• 주어진 문제의 시간제한이 1초라면 C++기준 약 1억번의 연산이 가능하다. 플로이드-워셜 알고리즘의 시간복잡도가 O(N^3)이므로 노드의 개수가 1억의 세제곱근 약 500개 이하정도라면 플로이드 워셜 알고리즘으로 문제를 해결할 수 있다.