최소 공통 조상 알고리즘 (Lowest Common Ancestor, LCA)
LCA 알고리즘은 트리(Tree) 자료구조에서 두 노드의 가장 가까운 조상을 찾는 알고리즘이다.
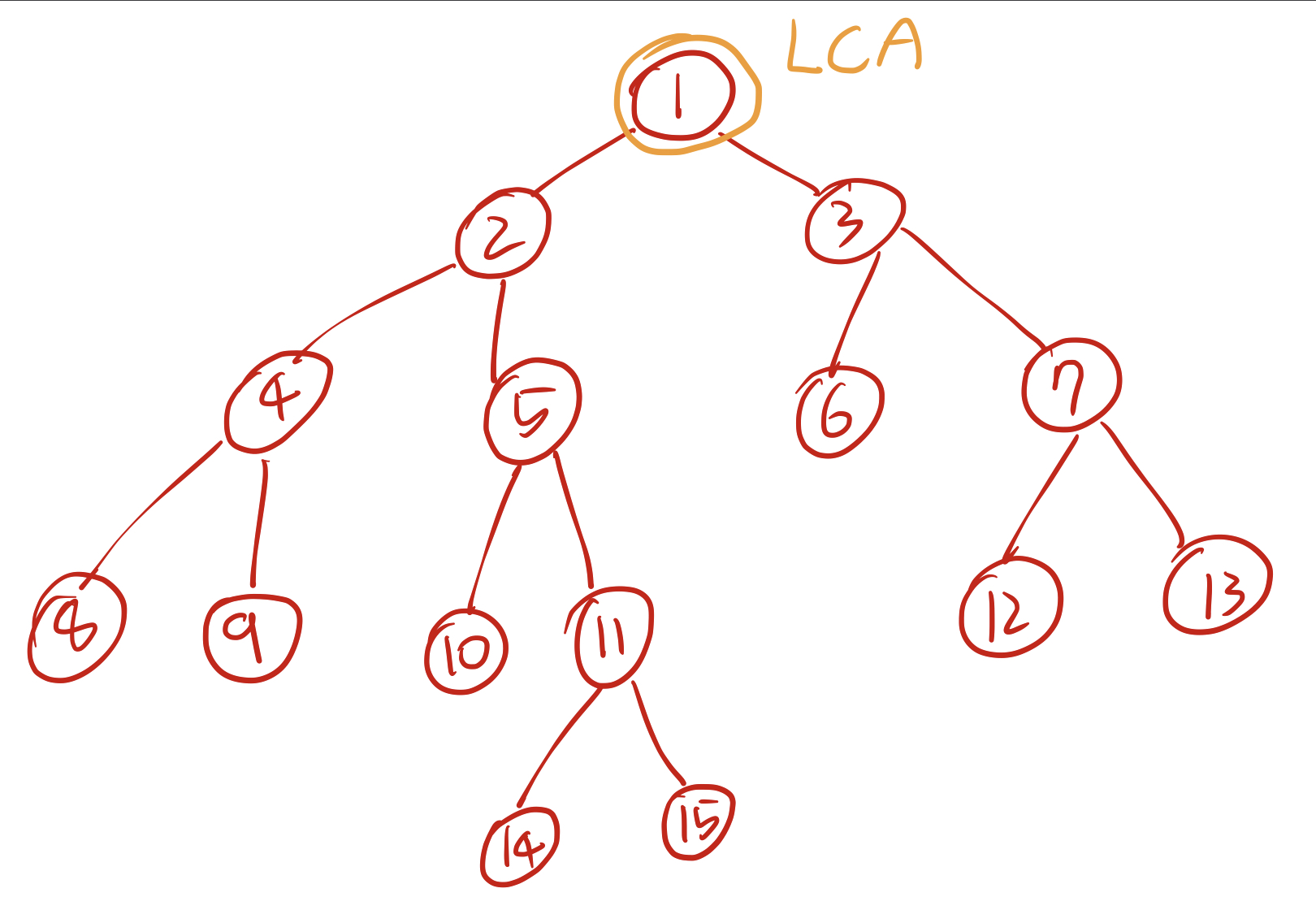
예를 들어 다음 그림을 보자.
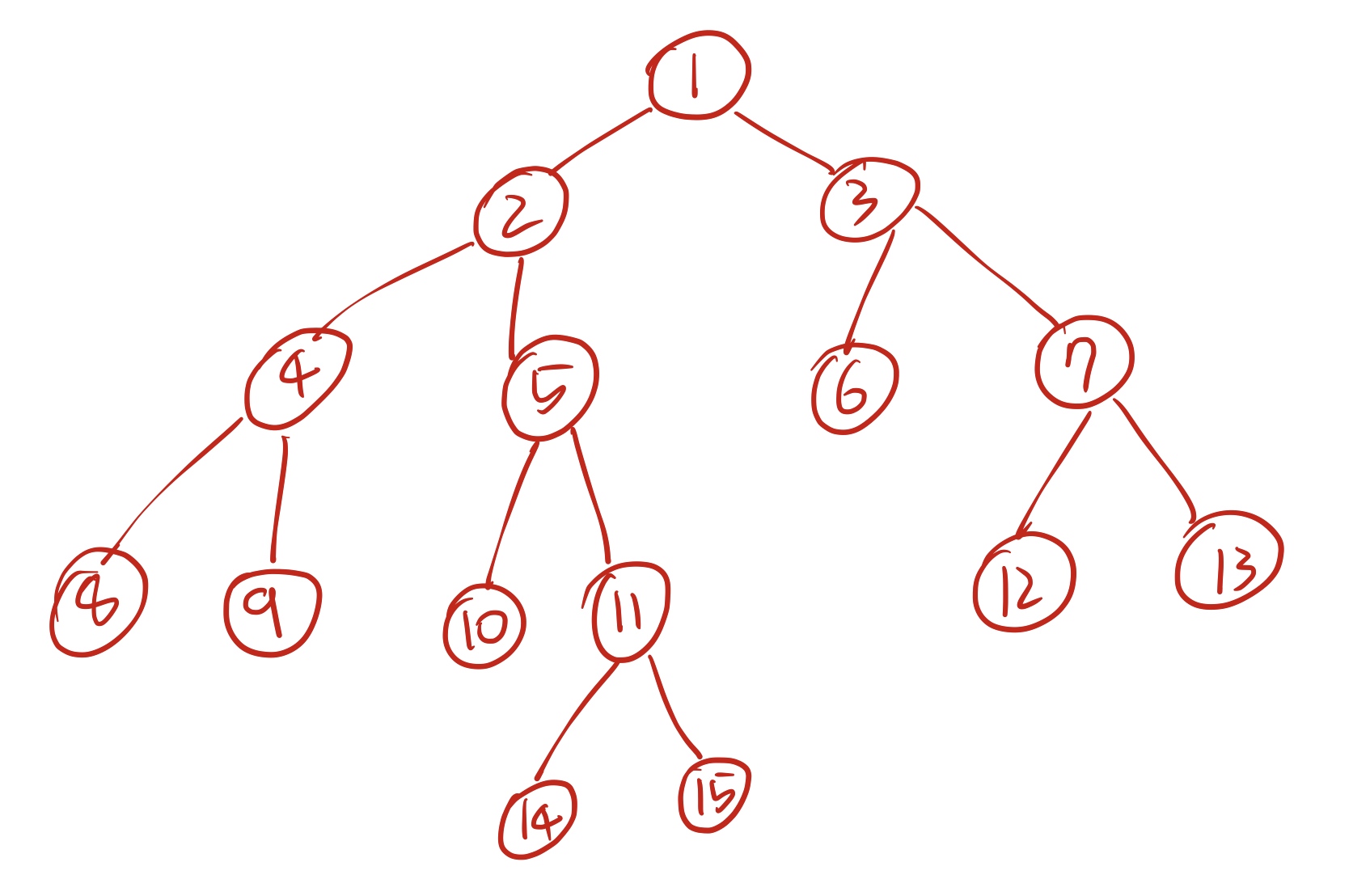
이 트리에서 8번 노드와 11번 노드의 최소공통조상(이하 LCA)은 2번 노드, 6번 노드와 13번 노드의 LCA는 3번노드, 15번 노드와 6번 노드의 LCA는 1번 노드이다. 그림으로 살펴보면 다음과 같다.
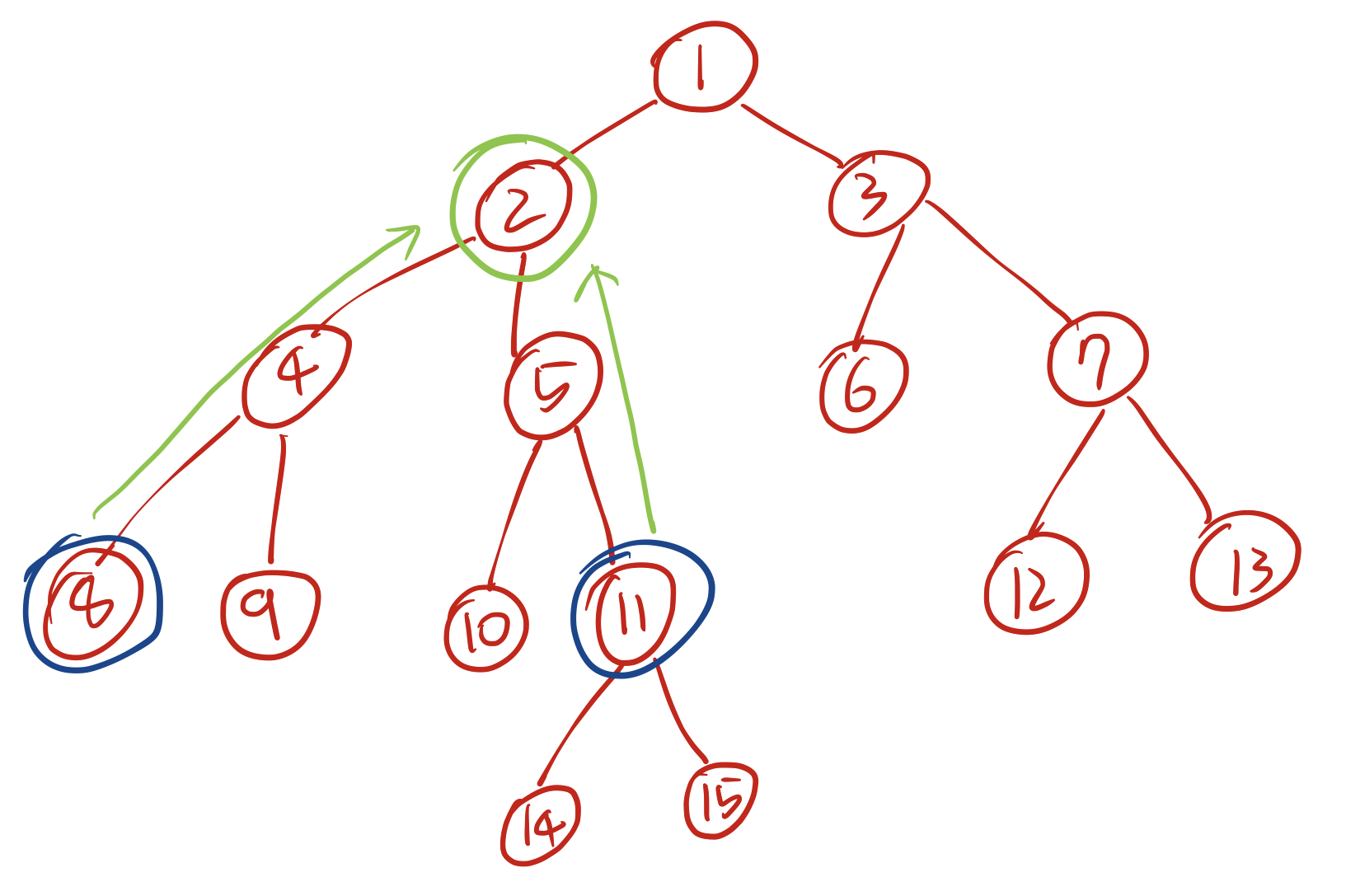
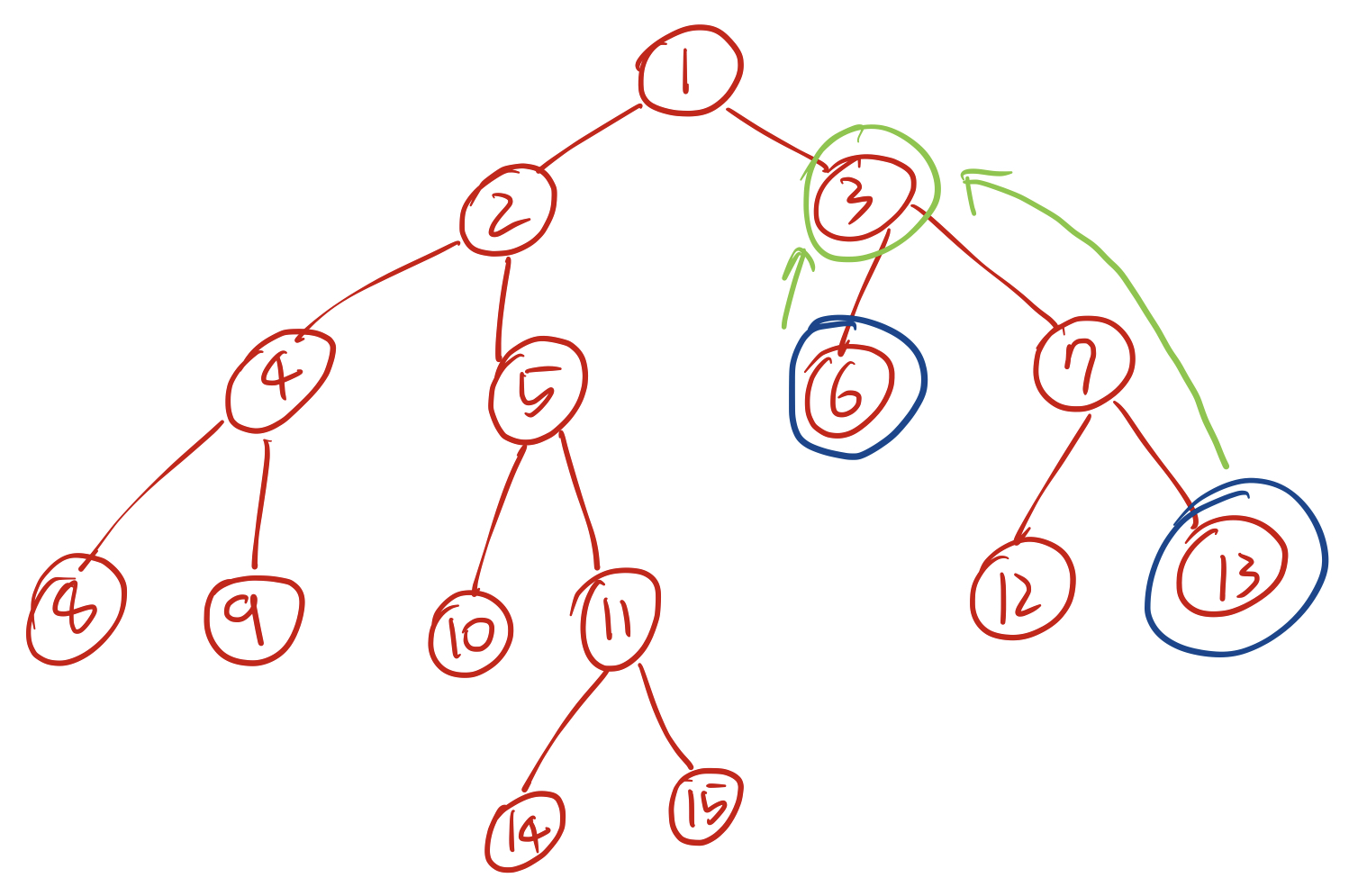
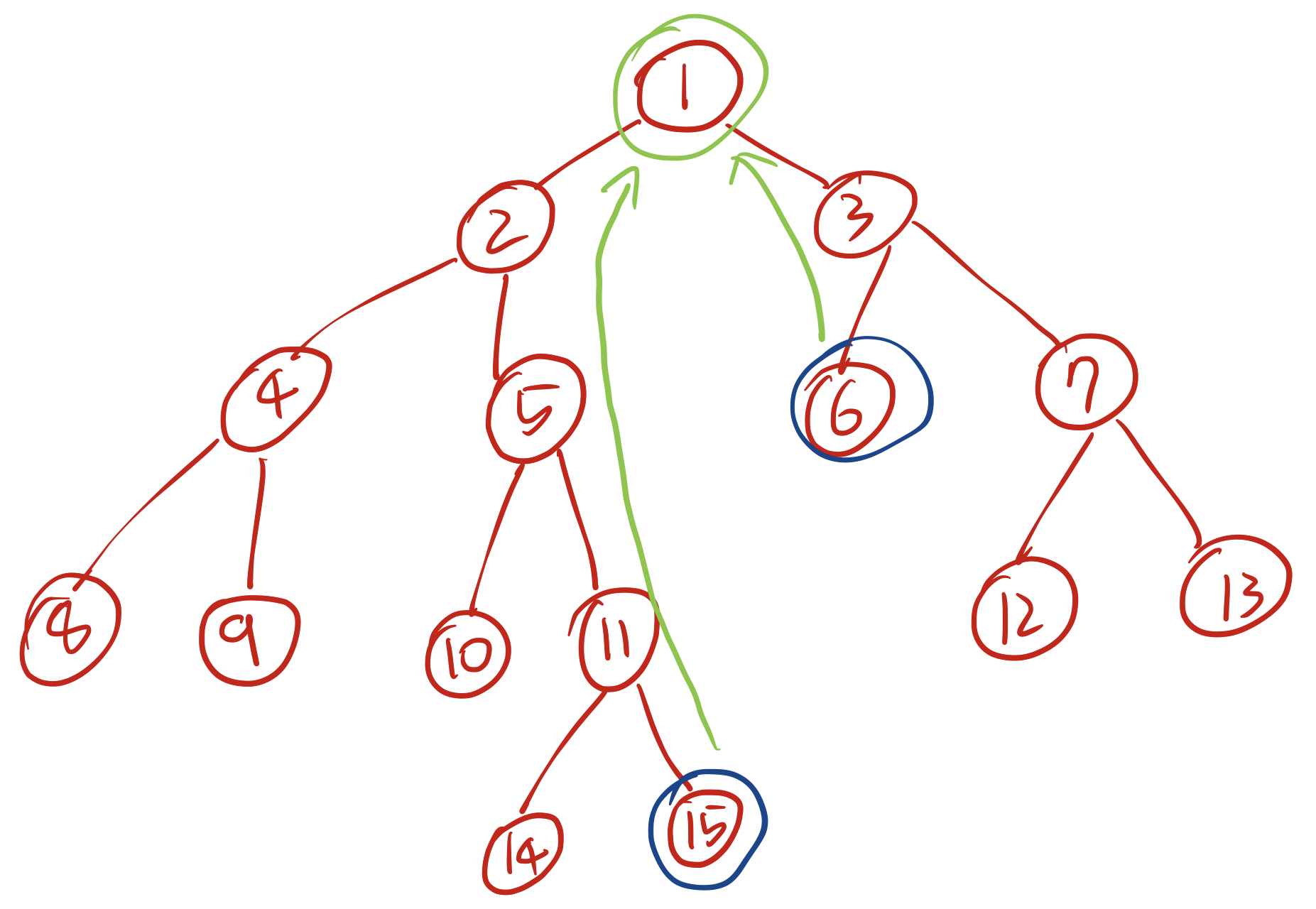
8번 노드 11번 노드 6번 노드 13번 노드 6번 노드 15번 노드
사람은 트리를 보면 바로 LCA를 쉽게 알아낼 수 있지만 이를 알고리즘으로, 또 효율적으로 계산해내려면 어떤 방법을 사용해야 할까? LCA를 찾는 알고리즘에는 두가지 방법이 있다.
LCA1
LCA를 찾는 첫번째 알고리즘은 매우 단순하다. 알고리즘은 다음의 순서를 거쳐 진행된다
- LCA를 찾고자 하는 두 노드의 깊이가 같아질때까지 깊이가 더 낮은 노드를 그 노드의 부모로 업데이트한다.
- 두 노드가 같아질때까지 각 노드를 각 노드의 부모로 업데이트한다.
그림으로 먼저 예시를 들어보겠다.
위 트리에서 14번 노드와 7번 노드의 LCA를 찾고싶다고 가정해보자.
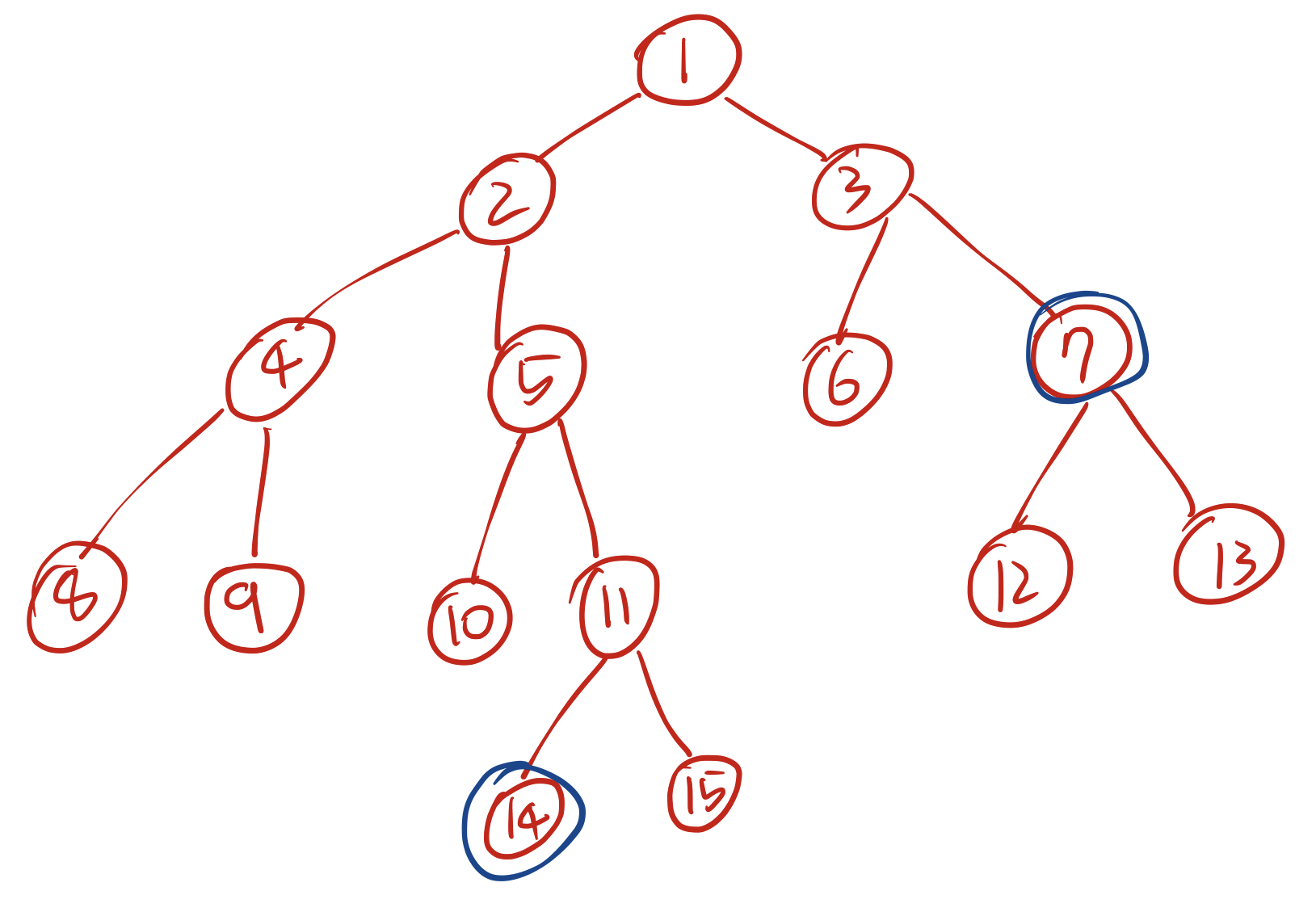
14번 노드와 7번노드의 깊이는 각각 4와 2로 서로 다르기 때문에 1번 과정을 수행한다. 1번과정을 한 번 수행하면
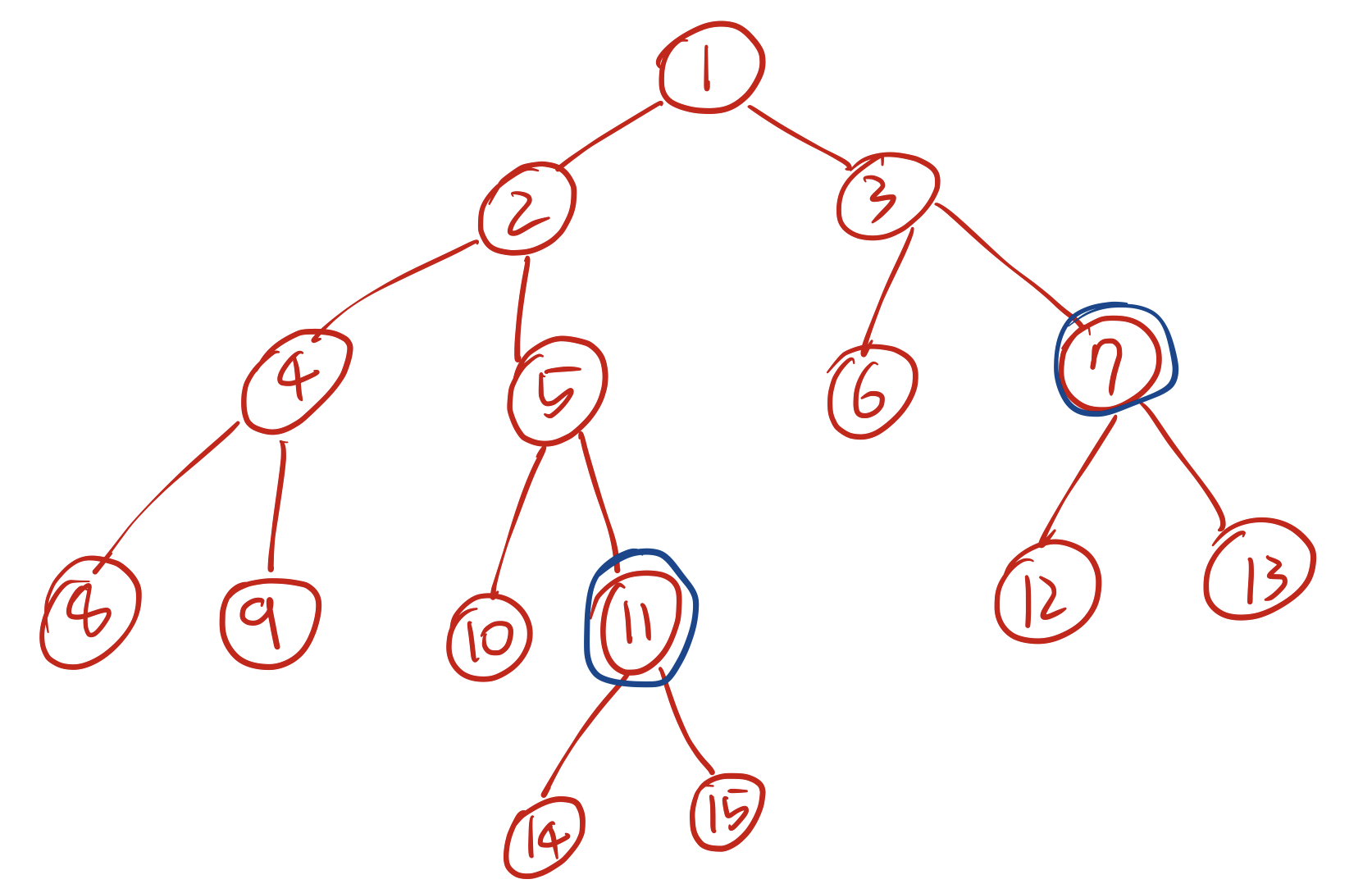
깊이가 4로 더 깊은 14번 노드를 14번 노드의 부모인 11번 노드로 업데이트한다. 그래도 깊이가 여전히 다르기 때문에 1번 과정을 한 번 더 수행한다.
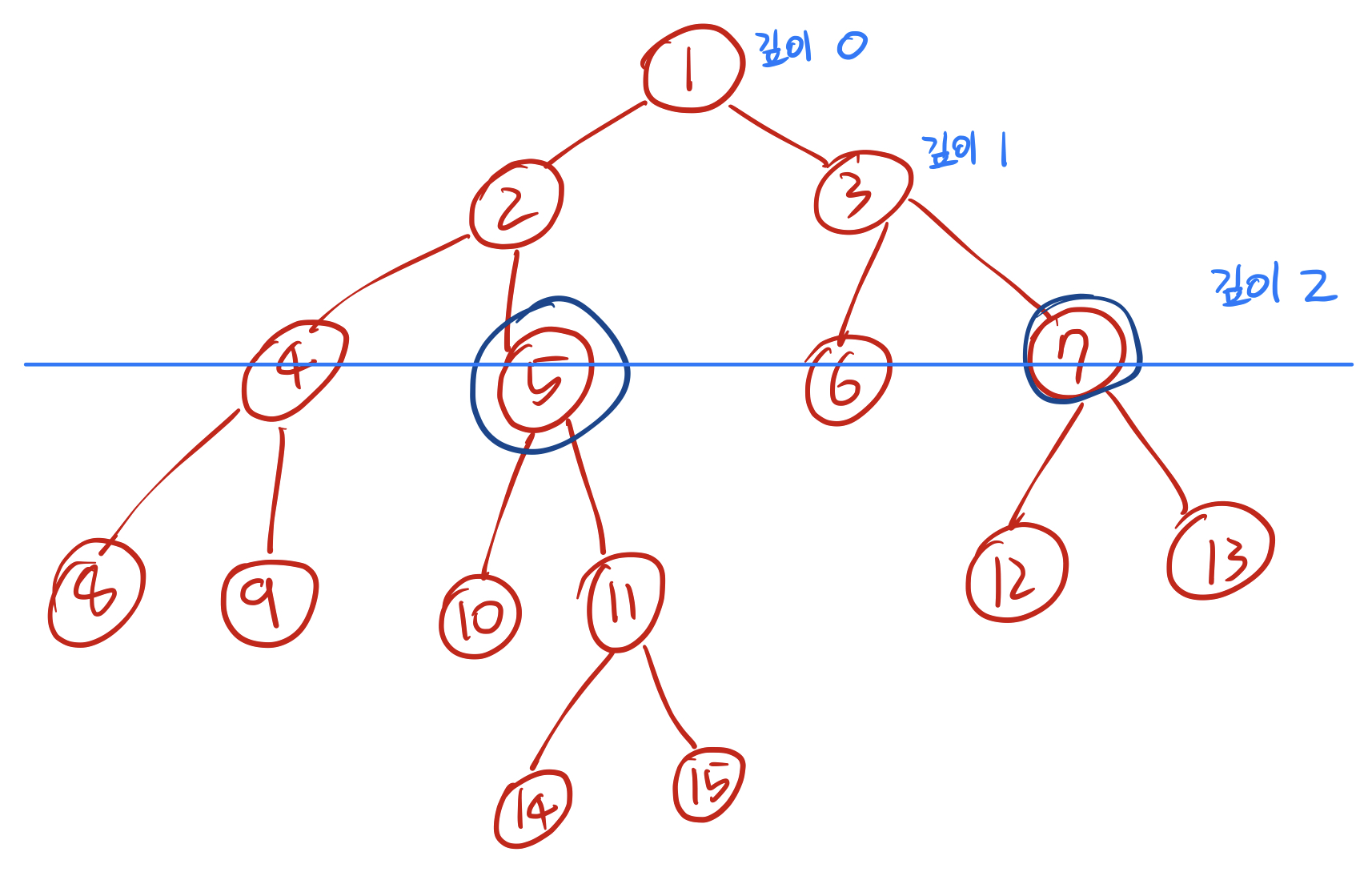
깊이가 3으로 더 깊은 11번 노드를 11번 노드의 부모인 5번 노드로 업데이트하면 비로소 깊이가 2로 7번 노드와 같아진다. 이제 2번 과정을 수행할 차례이다.
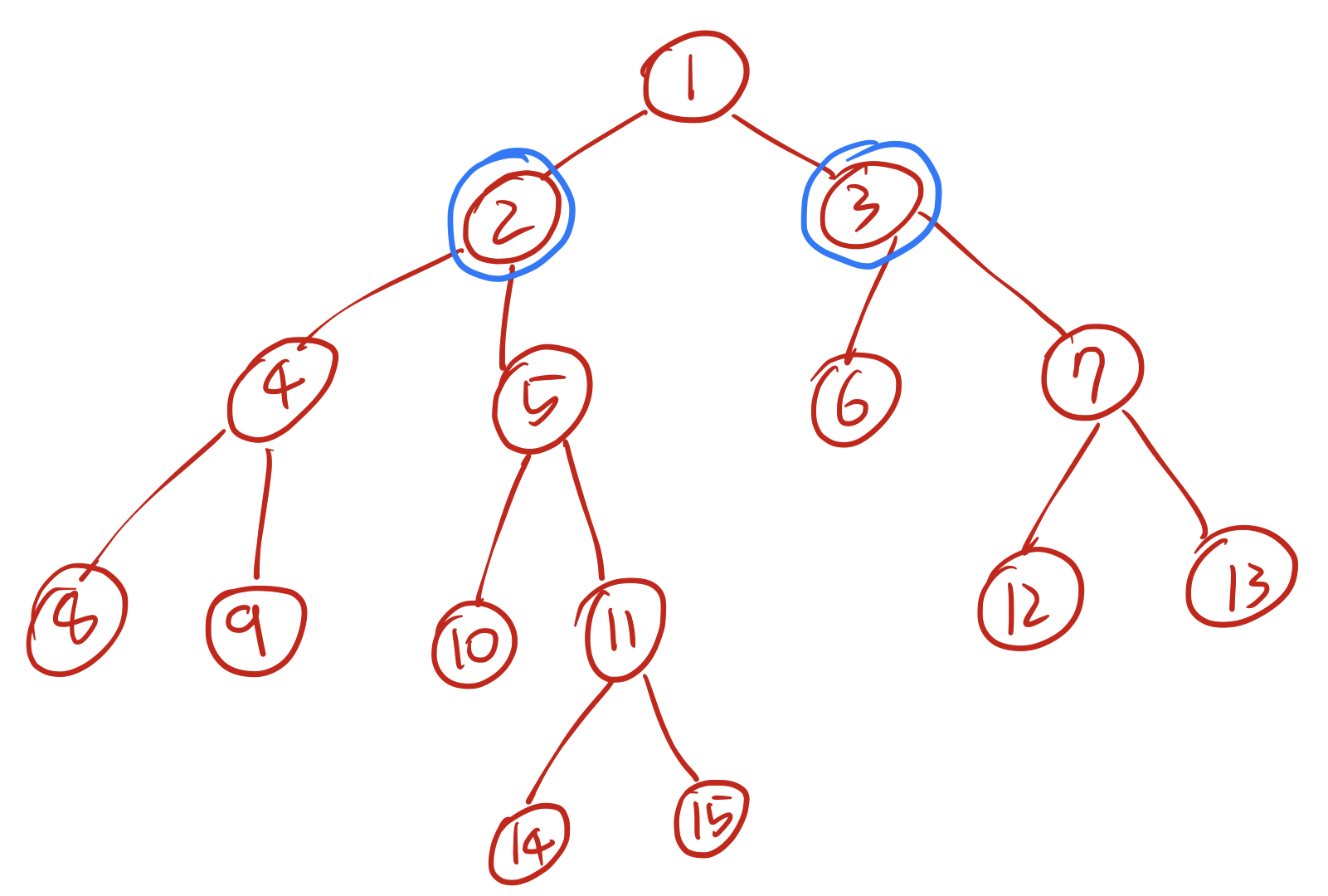
각각 5번 노드는 5번노드의 부모인 2번노드로, 7번 노드는 7번노드의 부모인 3번노드로 업데이트한다. 그래도 두 노드가 서로 같지 않기 때문에 2번 과정을 한 번 더 수행한다.
2번 과정을 한 번 더 수행하면 2번 노드는 1번 노드로, 3번 노드는 1번 노드로 업데이트 되고 비로소 1번 노드로 같아진다. 이렇게 모이게 된 한 노드가 바로 처음 우리가 찾던 14번 노드와 7번 노드의 LCA이다. 이제 이를 코드로 구현해보자.
LCA1의 구현
먼저 트리를 입력받고, 각 노드의 깊이를 모두 구해준다. 그 후 두 노드의 깊이가 같아질 때까지 한 노드를 그 노드의 부모로 업데이트하고, 깊이가 같아지면 두 노드가 같아질 때까지 깊이를 한칸씩 끌어올리면 (그 노드를 부모로 업데이트) LCA를 구할 수 있다.
각 노드의 깊이를 구할 때는 DFS를 이용한다. 모든 노드의 깊이를 담을 배열(depth)과 깊이를 구한 노드인지 체크할 방문 배열(Visit), 부모를 기록할 배열(parent)을 선언해준다. 그 후 DFS의 깊이와 부모 노드를 기록하면서 재귀를 들어간다.
void dfs(int node, int d) {
depth[node] = d;
Visit[node] = 1;
for (auto &i : Edges[node]) {
if (!Visit[i]) {
parent[i] = node;
dfs(i, d + 1);
}
}
}
트리를 양방향으로 입력 받아 넣었기 때문에 방문배열로 체크해주지 않으면 무한루프에 빠진다.
이렇게 모든 노드의 깊이와 부모 노드를 구했다면 이제 LCA를 구할 수 있다.
int LCA(int a, int b) {
if (depth[a] > depth[b]) swap(a, b);
while (depth[a] != depth[b]) b = parent[b];
while (a != b) {
a = parent[a];
b = parent[b];
}
return a;
}
a번 노드와 b번 노드의 LCA를 구하는 LCA함수이다. a번 노드보다 b번 노드의 깊이가 깊도록 고정하기 위해 조건문과 swap을 활용해 a,b 를 설정해준다.
그 후는 위에서 설명했던 과정을 코드로 옮겨놓은 것이다.
첫번째 while문은 깊이를 맞춰주는 과정, 두번째 while문은 두 노드가 같아질때까지 노드를 업데이트 하는 과정이다.
전체코드
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<int> Edges[50'505];
int depth[50'505];
int Visit[50'505];
int parent[50'505];
void dfs(int node, int d) {
depth[node] = d;
Visit[node] = 1;
for (auto &i : Edges[node]) {
if (!Visit[i]) {
parent[i] = node;
dfs(i, d + 1);
}
}
}
int LCA(int a, int b) {
if (depth[a] > depth[b]) swap(a, b);
while (depth[a] != depth[b]) b = parent[b];
while (a != b) {
a = parent[a];
b = parent[b];
}
return a;
}
int main(void) {
cin.tie(nullptr)->ios::sync_with_stdio(false);
cin >> N;
int a, b;
for (int i = 0; i < N - 1; i++) {
cin >> a >> b;
Edges[a].push_back(b);
Edges[b].push_back(a);
}
dfs(1, 0);
cin >> M;
for (int i = 0; i < M; i++) {
cin >> a >> b;
cout << LCA(a, b) << "\n";
}
return 0;
}
LCA1의 시간복잡도
LCA의 첫번째 알고리즘은 매 쿼리마다 부모 방향으로 거슬러 올라가기 위해 최악의 경우 O(N)의 시간복잡도가 요구된다.
따라서 모든 쿼리를 처리할 때의 시간복잡도는 O(NM)이다.
(N : 노드 개수, M : 쿼리 개수)
길이 너무 길어져 LCA의 두번째 알고리즘은 다음 글에서 설명하겠다.
참고 내용 출처 — https://www.youtube.com/watch?v=O895NbxirM8&ab_channel=%EB%8F%99%EB%B9%88%EB%82%98/

Leave a comment