최소 공통 조상 알고리즘 2 (Lowest Common Ancestor, LCA)
이전 글에서 설명했던 LCA 알고리즘의 방법 중 두번째 알고리즘을 설명하겠다. 첫번째 방법은 이해도 쉽고 구현도 간단하나 최종 O(NM)의 시간복잡도로 시간이 너무 오래 걸린다는 단점이 있다. 이를 최적화 하는 방법을 알아보자.
첫번째 알고리즘이 O(NM)이 걸린 이유는 부모를 거슬러 올라가는데 최악의 경우 O(N)의 시간이 소요되었기 때문이다. 따라서 시간을 줄이기 위해서는 이를 최적화해야만 한다. 이때 DP를 이용하면 시간복잡도를 크게 줄일 수 있다.
다음 예시를 보자.
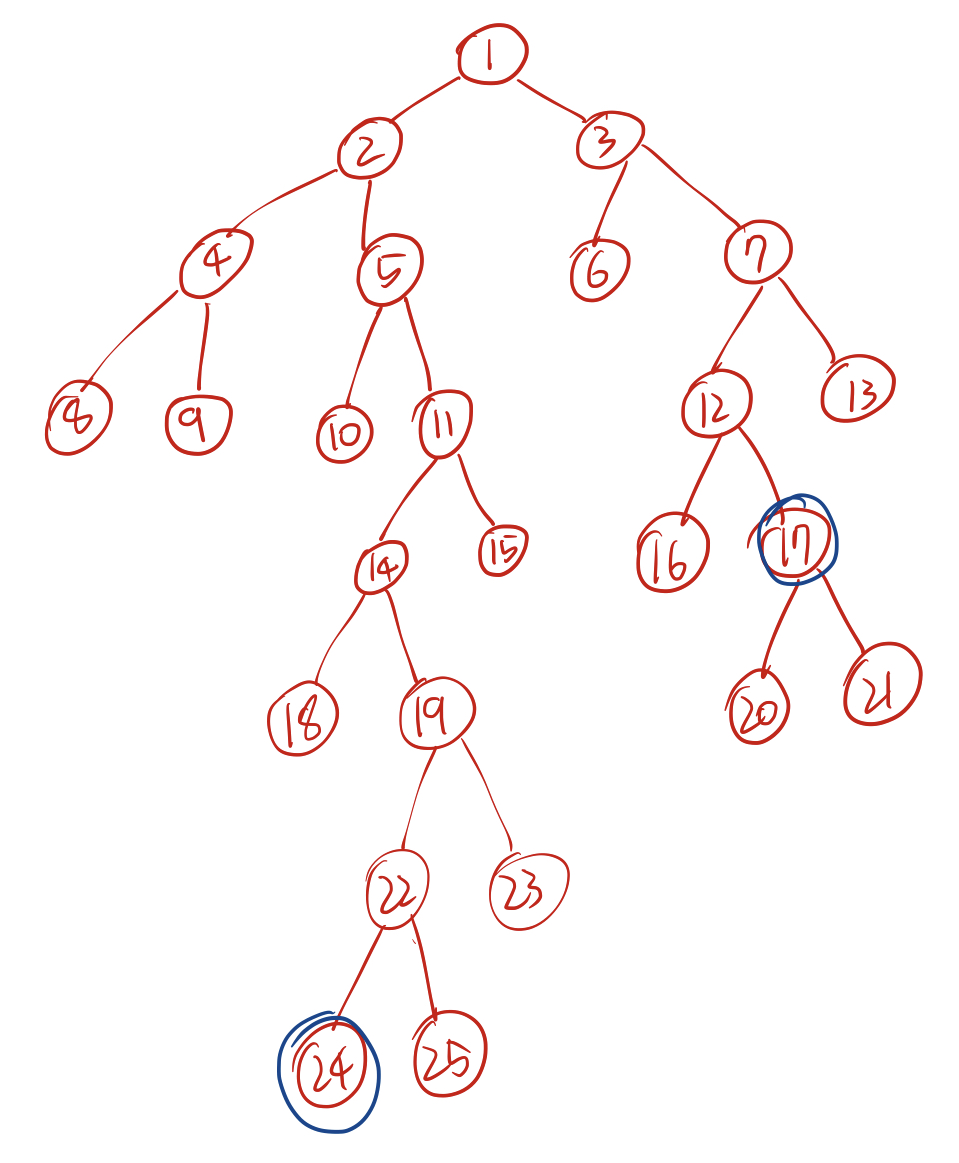
위 트리에서 24번 노드와 17번 노드의 LCA를 구한다고 가정해보자. 이때 첫번째 알고리즘에서는 부모노드를 하나씩 거슬러 올라갔지만 이번 알고리즘에서는 2의 제곱수만큼 거슬러 올라가보는 것이다. 이를 위해서는 모든 노드에 대해 각각 2의 제곱수 부모를 기억하는 배열을 만들어주어야 한다. 모든 각각의 노드에 대해서 첫번째 부모(2^0), 두번째 부모(2^1), 네번째 부모(2^2), 여덟번째 부모(2^3), … 을 기억하는 것이다. 이를 구할 때 DP를 이용한다.
각 노드의 2의 제곱수 부모를 구하기 위해 규칙을 잘 생각해보면
어떤 노드 A의 부모는 DFS를 통해 구할 수 있다.
A의 두번째 부모는 A의 부모의 부모이다.
A의 네번째 부모는 A의 두번째 부모의 두번째 부모이다.
A의 8번째 부모는 A의 네번째 부모의 네번째 부모이다.
A의 16번째 부모는 A의 8번째 부모의 8번째 부모이다.
…
parent[J][I]의 값이 J번째 노드의 (2^I)번째 부모노드라고 하자. 위 규칙의 점화식을 써보면
parent[J][I] = parent[parent[J][I-1]][I-1] 임을 알 수 있다.
다음부터는 코드를 보며 설명하겠다.
LCA2의 구현
먼저 부모배열의 값을 채워넣는 부분이다.
void dfs(int node, int d) {
depth[node] = d;
Visit[node] = 1;
for (auto &i : Edges[node]) {
if (!Visit[i]) {
parent[i][0] = node;
dfs(i, d + 1);
}
}
}
void setParent() {
dfs(1, 0);
for (int i = 1; i < 22; i++)
for (int j = 1; j <= N; j++) {
parent[j][i] = parent[parent[j][i - 1]][i - 1];
}
}
먼저 dfs 함수는 첫번째 LCA 알고리즘에서 구현한 것과 거의 동일하다. 다만 첫번째 알고리즘의 부모배열과 지금 알고리즘의 부모배열이 조금 달라졌는데, 전에는 첫번째 부모의 값만 기억하면 되어서 일차원 배열이었지만 이제는 2의 제곱수 부모들을 모두 기억해주어야 하기 때문에 2차원 배열이고, 따라서 이번 dfs에서는 parent[i][0] (i번째 노드의 2^0번째 부모) 의 값을 채워준다.
다음으로 setParent 함수에서는 모든 노드의 2의 제곱수 부모를 DP를 통해 채워준다.
이 문제에서는 N이 100,000으로 log를 구해보면 약 20부근이기 때문에 parent배열도 parent[101’010][22]정도로 선언해주었고 따라서 i도 1부터 22까지 증가시켜주었다. 아까 살펴본 점화식대로 부모배열을 채워준다.
다음으로 LCA 쿼리를 수행하는 LCA 함수이다.
int LCA(int a, int b) {
if (depth[a] > depth[b]) swap(a, b);
for (int i = 21; i >= 0; i--)
if (depth[b] - depth[a] >= (1 << i)) b = parent[b][i];
if (a == b) return a;
for (int i = 21; i >= 0; i--)
if (parent[a][i] != parent[b][i]) {
a = parent[a][i];
b = parent[b][i];
}
return parent[a][0];
}
첫번째 알고리즘과 마찬가지로 b의 깊이가 더 깊도록 조건문과 swap을 통해 a, b를 설정해준다.
첫번째 for문은 두 노드의 깊이를 맞추는 과정이다. 첫번째 알고리즘에서는 하나씩 올라갔지만 이번에는 2의 제곱수만큼씩 올라가본다. i를 N의 log부터 0까지 (0포함) 1씩 감소시키면서 a와 b의 깊이 차이가 1 « i 보다 크거나 같으면 b를 parent[b][i]로 업데이트한다. (1 « i 는 2^i 를 나타내는 것이다.)
깊이차를 제일 큰 2의 제곱수부터 차례로 채워나간다고 생각하면 쉽다. 예를 들어 깊이차가 11이었다면 채울 수 있는 가장 큰 2의 제곱수는 8이다. 11에서 8을 채우면 3이남고, 3을 채울 수 있는 가장 큰 2의 제곱수는 2이므로 2를 채우면 1이남고 또 1을 채울 수 있는 가장 큰 2의 제곱수는 1이므로 1을 채우면 깊이차를 모두 채운 것이다.
맨 처음에 들었던 예시를 보자.
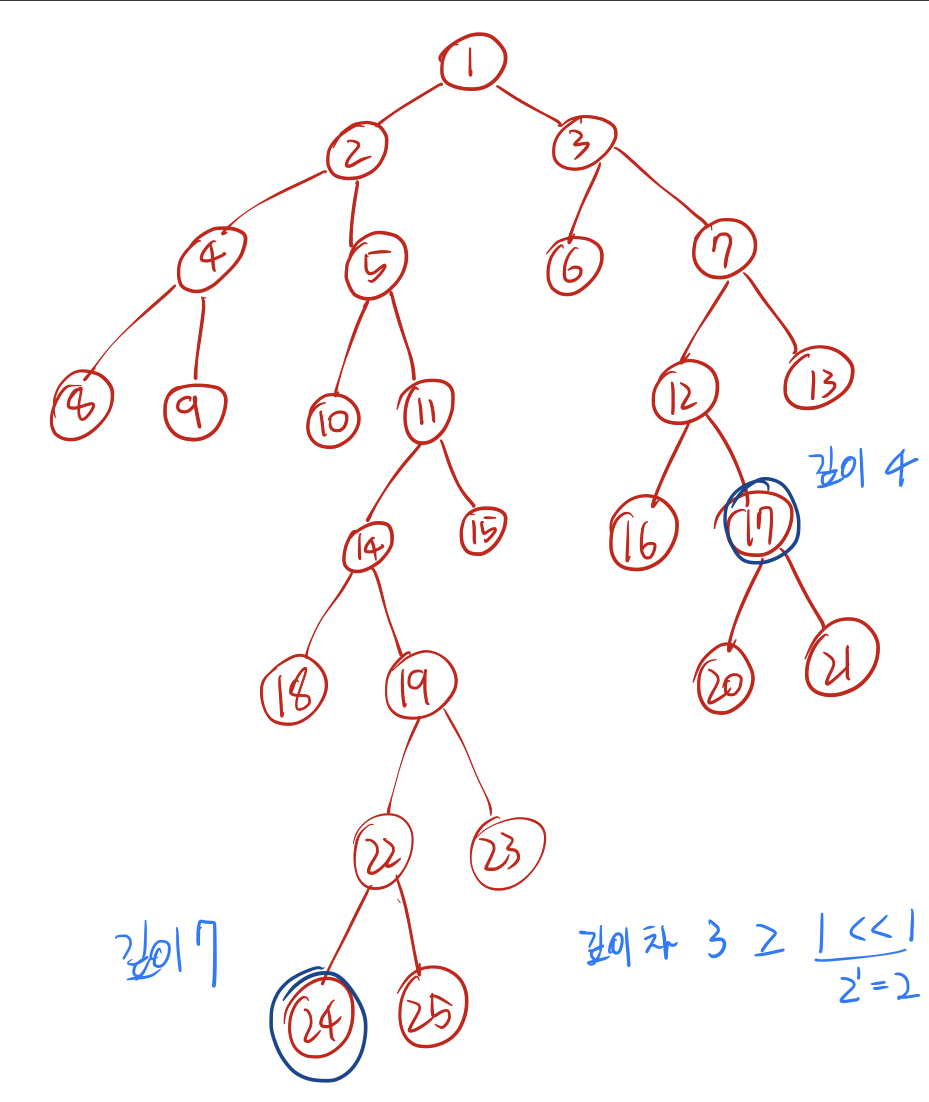
깊이차가 3이므로 채울 수 있는 가장 큰 2의 제곱수는 2이다. 따라서 24번 노드를 두번째 부모인 19번 노드로 올린다.
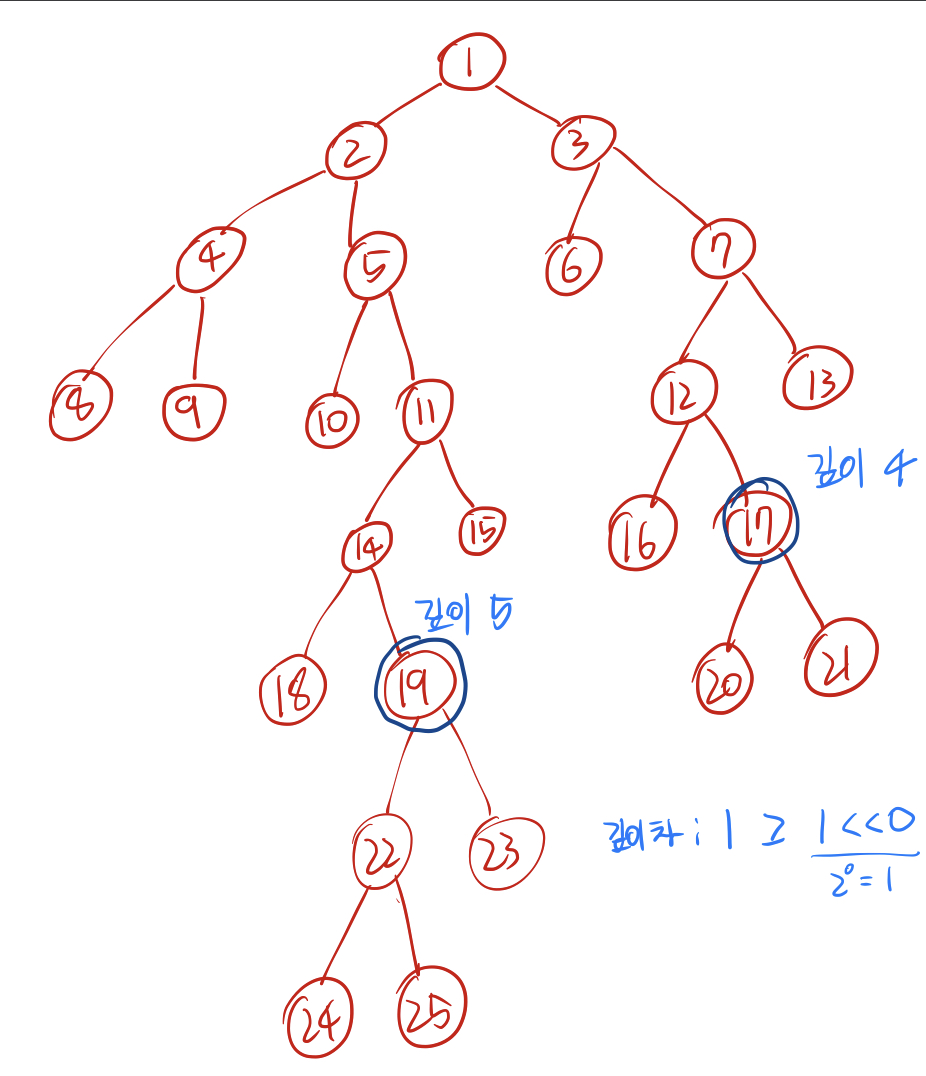
깊이차가 1이므로 채울 수 있는 가장 큰 2의 제곱수는 1이다. 따라서 19번 노드를 첫번째 부모인 14번 노드로 올린다.
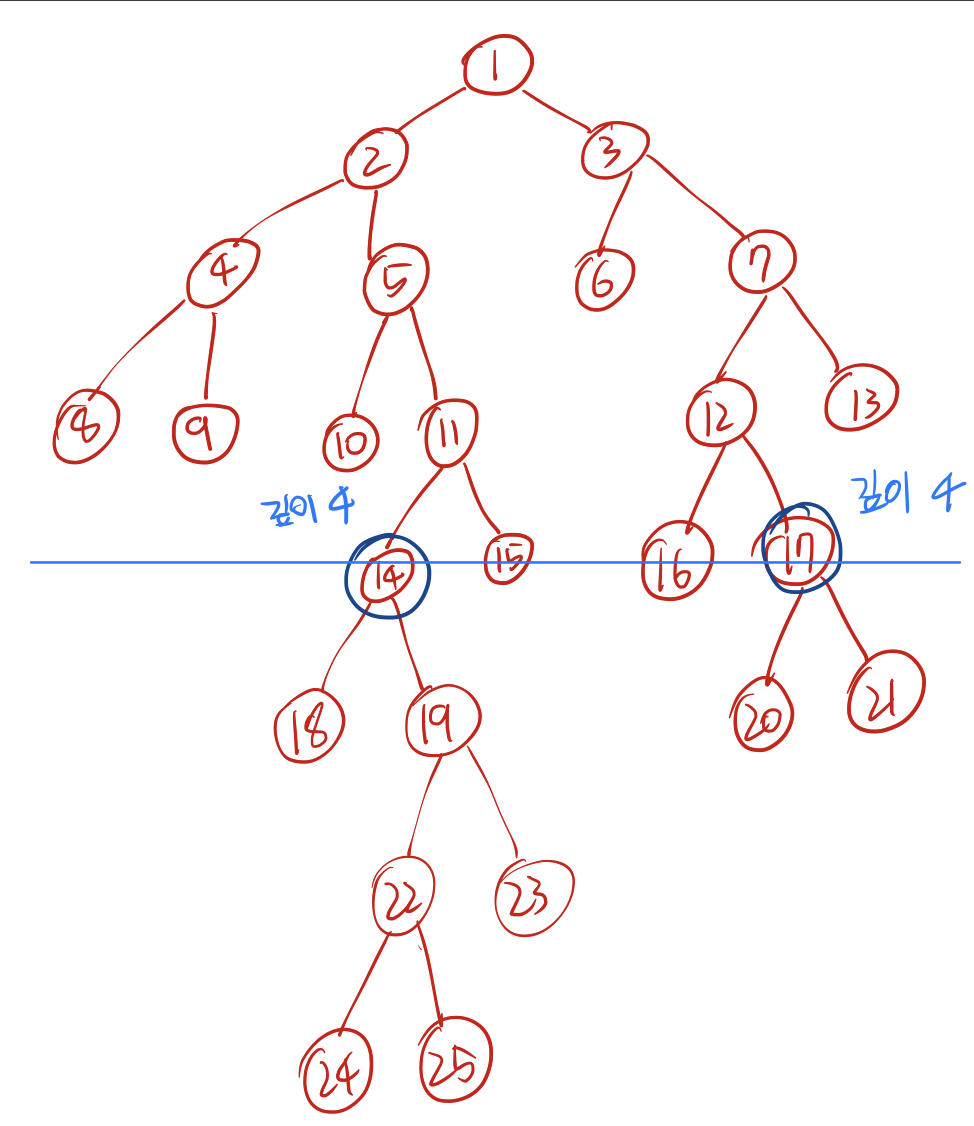
깊이가 마침내 같아졌고 만약 이때 두 노드가 같다면 그대로 리턴하면 된다.
두 노드가 다르다면 이제 두번째 for문을 실행할 차례이다.
for (int i = 21; i >= 0; i--)
if (parent[a][i] != parent[b][i]) {
a = parent[a][i];
b = parent[b][i];
}
두번째 for문은 i를 N의 log에서부터 0까지 감소시키면서 두 노드의 2의 i승 부모가 다른지 확인해보는 것이다. 만약 두 부모가 다르다면 LCA까지 올라갈 공간이 있다는 것이므로 두 노드 모두 올려준다.
위 예시에서 14번 노드와 17번 노드의 2의 제곱수 부모를 생각해보자. 두 노드 모두 2^21번째 부모부터 2^3번째 부모까지는 0으로 같다. 2^2번째 부모도 1번 노드로 같다. 2^1번째 부모부터 드디어 값이 달라지는데, 14번 노드의 2^1번째 부모는 5번 노드, 17번 노드의 2^1번째 부모는 7번 노드로 다르다. 따라서 두 노드 모두 각각 5번 노드, 17번 노드로 값을 업데이트해준다.
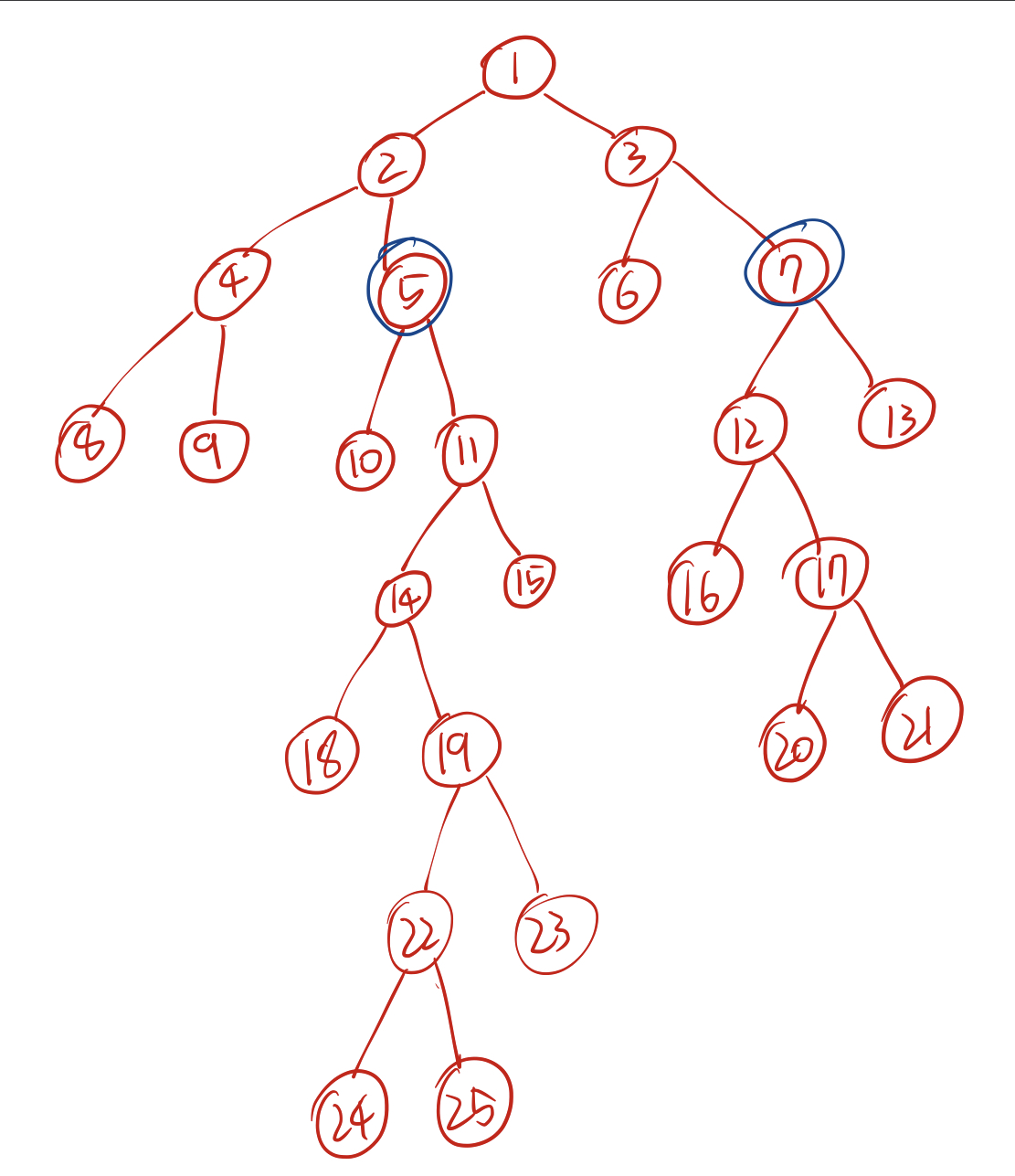
그 다음을 생각해보면 같은 과정을 거친다. 2^21번째 부모부터 2^1번째 부모까지는 값이 같으나 5번 노드의 2^0번째 부모는 2번 노드, 7번 노드의 2^0번째 부모는 3번 노드로 다르기 때문에 각각 업데이트 해준다.
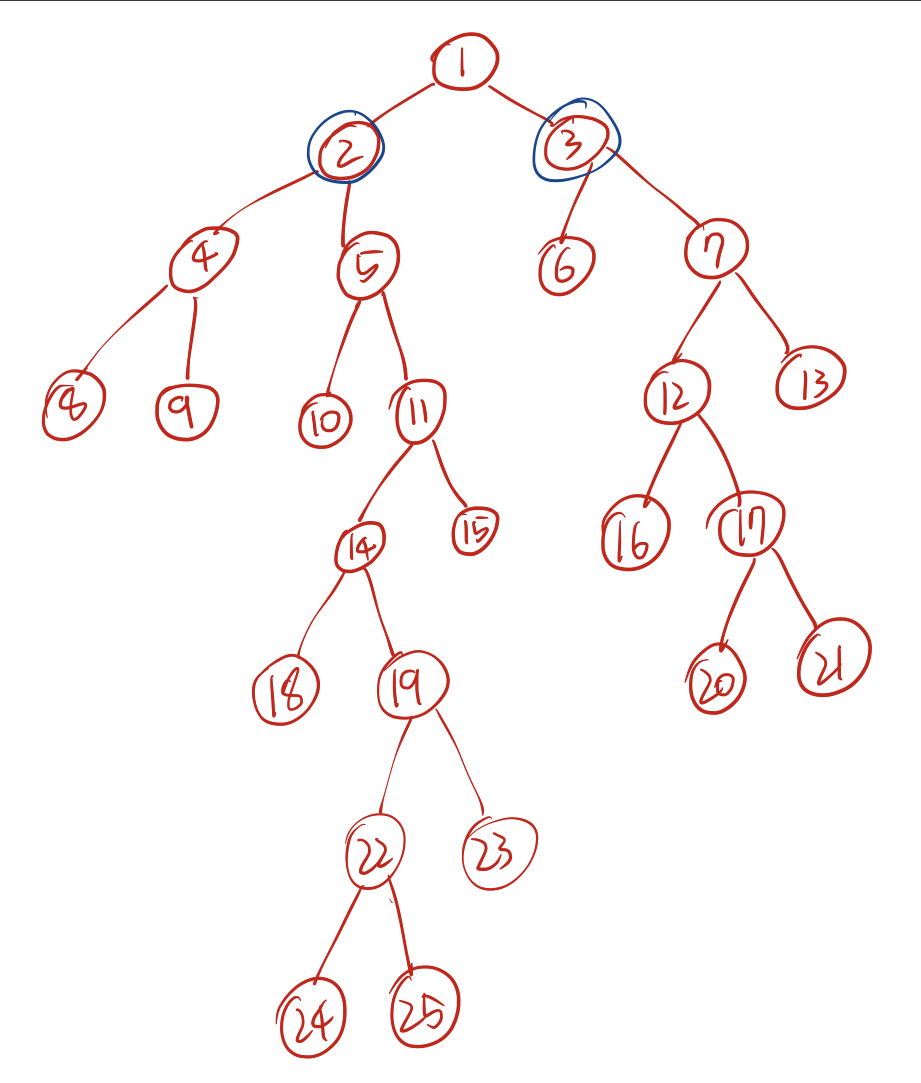
같은 과정으로 부모를 비교해보면 이번에는 모든 부모가 같기 때문에 값 변경없이 for문이 완료된다. 이 과정을 모두 거치고 나면 두 노드의 바로 위 첫번째 부모(parent[a][0])가 맨 처음 우리가 구하고자 했던 24번 노드와 17번 노드의 LCA가 된다.
전체코드
#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;
int N, M;
vector<int> Edges[101'010];
int depth[101'010];
int parent[101'010][22];
int Visit[101'010];
void dfs(int node, int d) {
depth[node] = d;
Visit[node] = 1;
for (auto &i : Edges[node]) {
if (!Visit[i]) {
parent[i][0] = node;
dfs(i, d + 1);
}
}
}
void setParent() {
dfs(1, 0);
for (int i = 1; i < 22; i++)
for (int j = 1; j <= N; j++) {
parent[j][i] = parent[parent[j][i - 1]][i - 1];
}
}
int LCA(int a, int b) {
if (depth[a] > depth[b]) swap(a, b);
for (int i = 21; i >= 0; i--)
if (depth[b] - depth[a] >= (1 << i)) b = parent[b][i];
if (a == b) return a;
for (int i = 21; i >= 0; i--)
if (parent[a][i] != parent[b][i]) {
a = parent[a][i];
b = parent[b][i];
}
return parent[a][0];
}
int main(void) {
cin.tie(nullptr)->ios::sync_with_stdio(false);
cin >> N;
int a, b;
for (int i = 0; i < N - 1; i++) {
cin >> a >> b;
Edges[a].push_back(b);
Edges[b].push_back(a);
}
setParent();
cin >> M;
for (int i = 0; i < M; i++) {
cin >> a >> b;
cout << LCA(a, b) << "\n";
}
return 0;
}
LCA2의 시간복잡도
LCA의 두번째 알고리즘은 매 쿼리마다 부모를 거슬러 올라가기 위해 O(logN)의 복잡도가 필요하다. 따라서 모든 쿼리를 처리할 때의 시간 복잡도는 O(MlogN)임을 알 수 있다. (N : 노드 개수, M : 쿼리 개수)
결론
LCA 두번째 알고리즘이 발상과 구현은 조금더 어려우나 시간관점에서 많은 절약을 할 수 있음을 알 수있다. 물론 두번째 알고리즘이 첫번째 알고리즘보다 더 많은 부모 노드를 기억해야하기 때문에 메모리관점에서는 손해를 본다. 두 알고리즘 모두 연습이 많이 필요할 것이다.
참고 내용 출처 — https://www.youtube.com/watch?v=O895NbxirM8&ab_channel=%EB%8F%99%EB%B9%88%EB%82%98/

Leave a comment